
家庭教師のAGENT-福岡県ブログ
家庭教師のAGENT<福岡県版>の情報発信。
福岡県での傾向やここだけのローカルな情報、耳より情報などをご案内します。
福岡県での傾向やここだけのローカルな情報、耳より情報などをご案内します。
福岡県公立高校入試-数学-入試傾向
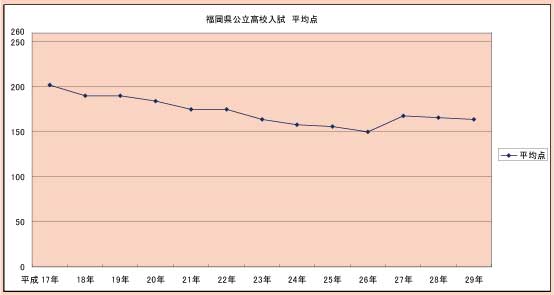
■傾向
例年、大問6題の構成で総問題数は20問程度です。
難問も含まれてるので45分の時間の使い方に慣れておきましょう。
ここ数年各大問の出題内容は固定されていますので、過去問を必ずチェックしておきましょう。
1・2問難しい問題が出てきますが。多くの問題は教科書の計算問題ができれば解ける問題です。
数学が苦手な人は計算だけでもかまわないので完璧にしておきましょう。
大問4・5・6の(1)は中学1年生でも解けるような簡単な問題であることが多いです。
数学が苦手な人や数学に勉強時間をかけても点数が伸びる気がしない人は、 大問1の対策以外は、中学1年生の内容だけでに的を絞って勉強をしてもいいかもしれません。
それをするだけで4割近くを狙えるようになります。
■対策
各分野の計算のルールや図形の基本性質は教科書に戻ってしっかりと確認しておくことが必要です。
数と式分野からは計算問題だけでなく、方程式の文章題、文字式と数の性質などが出題されています。
長文になっていることもありますが、時間をかけすぎず素早く情報を整理しましょう。
大問1は配点も3分の1以上を占めるので、速く確実に正解できるようになっておきましょう。
毎年出題される確率や資料の活用の分野も頻出です。中央値・最頻値などの意味を押さえておきましょう。
大問1は各分野の基本問題を集めた小問。
連立方程式の文章題、関数、平面図形、立体図形とバランスよく出題されます。
大問2以降の方程式の文章題は誘導形式が多いので取り組みやすですが、解く過程を書くことが求められます。
要領よく記述できるようになっておきましょう。
整数の性質も文字を使って説明させる問題が頻出です。
いろいろなパターンを練習して証明のコツを身につけておきましょう。
関数は、速さの変化などのグラフ問題、通る2点から直線の式を求める手順はこの分野では必須なので、 スパッと計算できるようにしておきましょう。
図形問題は難易度がやや高めです。
平面図形はこの数年は円が出題されています。
円周角を用いた相似の証明が必ず出ています。
立体図形は最短距離や立体の切断の問題が多く、方程式や三平方の定理を使った計算がスムーズにできるよう練習しておきましょう。
例年、大問6題の構成で総問題数は20問程度です。
難問も含まれてるので45分の時間の使い方に慣れておきましょう。
ここ数年各大問の出題内容は固定されていますので、過去問を必ずチェックしておきましょう。
1・2問難しい問題が出てきますが。多くの問題は教科書の計算問題ができれば解ける問題です。
数学が苦手な人は計算だけでもかまわないので完璧にしておきましょう。
大問4・5・6の(1)は中学1年生でも解けるような簡単な問題であることが多いです。
数学が苦手な人や数学に勉強時間をかけても点数が伸びる気がしない人は、 大問1の対策以外は、中学1年生の内容だけでに的を絞って勉強をしてもいいかもしれません。
それをするだけで4割近くを狙えるようになります。
■対策
各分野の計算のルールや図形の基本性質は教科書に戻ってしっかりと確認しておくことが必要です。
数と式分野からは計算問題だけでなく、方程式の文章題、文字式と数の性質などが出題されています。
長文になっていることもありますが、時間をかけすぎず素早く情報を整理しましょう。
大問1は配点も3分の1以上を占めるので、速く確実に正解できるようになっておきましょう。
毎年出題される確率や資料の活用の分野も頻出です。中央値・最頻値などの意味を押さえておきましょう。
大問1は各分野の基本問題を集めた小問。
連立方程式の文章題、関数、平面図形、立体図形とバランスよく出題されます。
大問2以降の方程式の文章題は誘導形式が多いので取り組みやすですが、解く過程を書くことが求められます。
要領よく記述できるようになっておきましょう。
整数の性質も文字を使って説明させる問題が頻出です。
いろいろなパターンを練習して証明のコツを身につけておきましょう。
関数は、速さの変化などのグラフ問題、通る2点から直線の式を求める手順はこの分野では必須なので、 スパッと計算できるようにしておきましょう。
図形問題は難易度がやや高めです。
平面図形はこの数年は円が出題されています。
円周角を用いた相似の証明が必ず出ています。
立体図形は最短距離や立体の切断の問題が多く、方程式や三平方の定理を使った計算がスムーズにできるよう練習しておきましょう。
福岡県公立高校入試-数学-年度別

家庭教師のエージェントでは、小学生、中学生、高校生と様々なコースをご用意しております。
中学校
久留米大附設中学校 西南学院中学校 福岡大学附属大濠中学校 福岡女学院中学校 明治学園中学校 筑紫女学園中学校 青雲中学校 ラ・サール中学校 上智福岡中学校 福岡教育大附属小倉中学校 弘学館中学校 東明館中学校 早稲田佐賀中学校
高校
福岡高 香住丘高 福岡中央高 筑紫中央高 明善高 福岡大附属大濠高 小倉高 八幡高 小倉西高 田川高 自由ヶ丘高 筑紫丘高 春日高 筑紫高 香椎高 八女高 西南学院高 東筑高 小倉南高 八幡南高 北九州高 東筑紫学園高 修猷館高 宗像高 筑前高 福翔高 久留米高 筑紫女学園高 北筑高 戸畑高 小倉東高 九国大附属高 城南高 新宮高 福岡西陵高 伝習館高 山門高 福岡大学附属若葉高 門司学園高 京都高 嘉穂高 明治学園高
大学
東京大学 京都大学 大阪大学 神戸大学 早稲田大学 慶應義塾大学 関西大学 関西学院大学 同志社大学 立命館大学 広島大学 山口大学 九州大学 長崎大学 熊本大学 大分大学 佐賀大学 福岡大学 西南学院大学 福岡教育大学 北九州市立大学


